Considering that the Second Viennese School of Composers was arguably the most influential individual school of compositional thought in the 20th century, and that the movement consisted of only three composers, one might reasonably expect that the entire small oeuvre of Webern works would have been by now well-worked and re-worked through by analysts. However, with respect to the atonal Six Bagatelles for String Quartet, Op. 9, such is not the case. One can only speculate as to why this is, but perhaps it is due in part to the fact that Webern’s serial music, with its rigid organization and strict adherence to tone-row organization (which became the guiding light for so many later serial composers), is easier to explain than his post-tonal but pre-serial works.
There exist only a handful of published analyses of individual movements of the Six Bagatelles, and only a few complete analyses. (I have recently been made aware of a newer article, written after this analysis was completed, by Benjamin K. Davies. This article can be found here.) The complete analyses include published work by Allen Forte1 and Richard Chrisman2, as well as yet unpublished doctoral dissertations by Jeffrey Perry3 and Carolyn Denise Mullin4. Three of these texts, the Forte, Chrisman, and Mullin, will provide topics for comparison in this paper. The current author knows of no published analyses that look at the second movement alone. What follows, then, is a very brief description of the methods employed by these three authors.5
Forte’s approach to pitch organization in the Bagatelles uses the octatonic scale, set-class 8-28, as the overarching structure from which subsets are created and individual harmonic fields generated. In his analysis of the second movement, Forte talks of a “dialectical tension” created by the juxtaposition of two, and sometimes all three, distinct members of set-class 8-28, made clear though the division of these sets by primarily accompanimental and melodic roles.6 Forte’s use of the octatonic scale as a way of describing the pitches in Webern’s Bagatelles is interesting if somewhat difficult to perceive when listening to the music. Composers comparatively more famous for using the octatonic scale, such as Stravinsky and Debussy (both of whom Forte himself cites early in his text) or even Messiaen, tend to use the collection of pitches in a much more blatant and obvious way, exploiting the eight notes in exclusion of the rest of the chromatic scale. In the second movement of Webern’s quartet, however, one could argue that the very properties that make the octatonic scale aurally recognizable are all but obliterated by the overlay of chromaticism. In spite of this fact, one cannot deny that on some level set-class 8-28 reflects a structural system of the movement.
In contrast to Forte, Chrisman’s analysis uses interval-class (IC) succession as a means to demonstrate how a select few set-classes are built up from first small cardinal sets of three or four pitches into larger collections of five and six pitch-classes, and vice-versa. A short example from his analysis will demonstrate:
Here Chrisman shows a passage in which set-class 4-8, a prominent set in the movement, is created by successive subtraction of pitches from set-class 6-38, first to the five note set 5-20, before arriving at 4-8. Most important here is the order in which those pitches are represented, shown in the interval arrays. Throughout the movement, patterns emerge which show that Webern uses specific interval orderings repeatedly, both in their normal and retrograde forms, to arrive at a select few set-classes.7
It is with Chrisman’s ideas in mind that Mullin expands upon patterns of interval succession with a bit more detail. Her analysis fills in some of the gaps of Chrisman’s article, while charting out measure by measure the additive or subtractive process by which each of the Kh related sets unfolds. Hence, she also places a heavy weight on the idea that interval arrays appear in one order during the initial part of the movement, and the retrograde of that array at the end of the movement.
While this type of analysis sheds light on certain organizational properties of the piece, there is a certain amount of data manipulation that must go into the pitch-class ordering to keep the arrays consistent throughout the movement. This can be seen in the above example, where Chrisman must first omit PC2 from set 5-20, but not PC4, to give the array listed by set 4-8. One could just as easily have done the reverse, but for the fact that the IC array would not fit the desired pattern. Perhaps this is splitting hairs, and there is certainly knowledge to be gained from recognizing some consistency in the order by which Webern moves from one set to another. But, suffice it to say that the process is not without its inconsistencies.
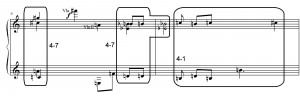
Both Chrisman and Mullin also refer to an analysis by Henri Pousseur in which he looks at the first movement as consisting of harmonic fields within which intervals are organized by a semitone-some other interval-semitone pattern.8 If one compares this idea with, for example, the list of four-note set-classes given for the second movement in the Mullin text, one can clearly find this pattern. All of the four-note sets outlined by Mullin, 4-7, 4-8, and 4-9, are made up of two IC1 separated by ICx, where x=some other interval (not including the “around-the-corner” interval).
But it is possible that the chromatic nature of the piece has been stressed too heavily, if one looks at both harmonic and linear manifestations of the pitch organization. A look at the opening melodic motive shows both IC5 and IC1, and IC5 is emphasized throughout the piece on both the micro and macro levels. Therefore, this analysis will show that this movement is also structured around sets consisting of IC5-some other interval-IC5. Further, by taking into account dynamics and register, the argument in favor of IC5 as a primary unifying force is strengthened. This is not to dispute the validity of the arguments made by the above authors, but rather to reexamine Webern’s music from a slightly different angle, and one which focuses more heavily on what can be perceived in the performance of the music. I will also argue that focusing more on how IC5 is used gives a clearer outline of the form of the movement—an aspect which has been overlooked in the above-mentioned analyses.
Let’s begin by scanning the entire movement to find IC5 working on the macro level. There are very few pitches in this movement marked at a dynamic higher than p or pp, but the few that are marked f and arco, save the final chord, form a four-note set, 4-8.
These pitches appear in the order IC5-IC1-IC5, thus outlining the perfect-fourth quality of the set. Even in a short movement such as this, the aural connection between one of these pitches and the next is admittedly difficult to hear; the outline of the fourths is disguised by the chromaticism of the context. Therefore it seems likely that the fourths are a unifying element for Webern’s compositional process as much as a part of the listening experience.
But IC5 shows up in more obvious places as well, and in contexts in which the interval is much more easily perceived. In the first measure of the movement, we hear the lowest pitch thus far, PC7 in the second violin move down a fifth to the lowest pitch of the entire movement, PC0, in the cello at the downbeat of measure 2. To emphasize the importance of this moment, I return to the Forte text and his discussion of Theodor Adorno’s claim that this movement is in effect a scherzo: Forte calls the scherzo idea an “apt characterization” of the movement, and further remarks that if it is a scherzo, than it has a “chronic limp compared to the traditional triple-metered scherzo.” If we take the “scherzo” idea with its awkward “limp” at face value, then perhaps Webern’s sense of humor is at work here, for the opening measure to the downbeat of measure 2 does have the feeling of a V-I cadence on C! The G-as-dominant effect is hammered home with the viola triplets, which give the “dominant” its “leading tone” in waltz-like rhythm against the second violin’s bass-note G. The emphasis here, however, is not on the tonal implications of the gesture. Rather the tonal hint is meant to reinforce IC5 as structural in and of itself, and the reference to tonality is to draw attention to the interval, and perhaps to give the listener the scherzo-like context in which to hear the movement.
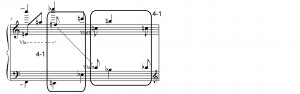
This gesture also serves the purpose of demarcating the end of the introductory material and the beginning of the transitory material of measure 2. (The use of PC0 to mark the end of a section is consistent with the first violin’s sffp C-natural at the end of the movement and, I will later argue, the viola’s middle-C in measure 6 to end the middle portion.) The four-note set-classes of measure 1 can be neatly divided into two sets of 4-7, a set whose largest interval is IC5, and which appears more than any other four-note set in the movement according to both Chrisman and Mullin. It seems more fitting in measure 1 to break these into smaller three-note sets in order to reflect the way that they are emphasized in the music. In this context, the opening violin motive is set-class 3-4 (0,1,5), the answer played one note each by the other three instruments is 3-5 (0,1,6). Each of these sets can be described as an IC5 with an adjacent IC1, and this is how they are presented in the music: that is, the violin motive begins by outlining the fourth, and the answer closes by outlining the fourth.9
Measure 2 works as a foil to measure 1, and uses IC1 as its main interval. But for the moment, we will ignore the rest of measure 2 and come back to it later, because we need further justification of the importance of IC5. Measures 3-6, which form the B section, provide evidence. First, in the melodic exchange between the two violins (a hocket-like idea), the pattern of IC5-ICx-IC5 forms a continuous chain, beginning with the pick-up on the and-of-five in measure 2 through the first beat of measure 5.
Much less obviously, similar relationships occur in the other parts as well, most notably with the interjection by the viola at the end of measure 4 and into measure 5. An analysis of the (primarily) melodic set-classes throughout this passage shows that the resultant sets are 4-20, 4-26, 4-8, with one appearance of 4-23. Thus, the sound that unfolds is one of a series of interlocking fourths.
Returning to measure 2, we find a harmonic context completely different from the IC5 idea. From beats 2 through 4, the first violin, viola, and cello parts collectively play set-class 4-1 (0,1,2,3), a completely chromatic tetrachord absent of IC5. This is the material that Webern uses to create a contrast, and which in turn helps to delineate the form of the movement. If measure 3 begins the B section, then the A section lasts from the beginning through measure 2 and provides in close succession the materials upon which the movement is structured. In fact, the two worlds collide on beat one of measure 2, in the form of set-class 5-Z37. When register is taken into account, we hear an IC5 in the lowest two voices (PC0 and PC5) and an IC5 in the upper voices (PC9 and PC2), with an IC1 (PC1) stuck in the middle. Without the C-sharp, the collection of pitches forms set 4-26 (which makes appearances in mm. 3-5). The C-sharp then interrupts the fourth-based harmony with a half-step, which then hands off to set-class 4-1. (If we include the C-sharp into this distinct four-note set, we have superset 5-1, again a cluster of semitones and devoid of IC5). The register of these pitches drives the point home: all four (or five) notes are played in the closest possible voicing.
Since the B section begins with the melodic outlining of IC5, we must look ahead to find where set-class 4-1 makes its reappearance. We find this moment in measure 5, beginning with beat 2. As in section A, here set-class 4-1 emerges out of the texture with a two-voice mirrored counterpoint between the first violin and cello.
Section B comes to a close with a cadence on the second half of beat one of measure 6, in a chord that forms set-class 4-7, and which, as mentioned above, features PC0 as its bass note. The reappearance of set-class 4-7 connects this moment to the opening gestures of measure 1, and the use of PC0 reinforces the cadential gesture by connecting the sonority to the C-natural on the downbeat of measure 2. In a sense, this chord is a result of the intersection between the chromatic and IC5-based sets, balancing the weight of heavy IC5 sets 4-26, 4-23, and 4-20 with IC1 heavy 4-1:
| Forte Number | Prime Form | IC Vector |
| 4-7 | (0,1,4,5) | 2 0 1 2 1 0 |
| 4-20 | (0,1,5,8) | 1 0 1 2 2 0 IC5-heavy set |
| 4-23 | (0,2,5,7) | 0 2 1 0 3 0 IC5-heavy set |
| 4-26 | (0,3,5,8) | 0 1 2 1 2 0 IC5-heavy set |
| 4-1 | (0,1,2,3) | 3 2 1 0 0 0 IC1-heavy set |
Having returned to set-class 4-7, Webern also returns to the opening section A idea in varied form. Measure 6 parallels measure 1, with material made primarily from set-class 4-7. Measure 7 parallels measure 2, built upon set-class 4-1. The motivic material is somewhat different, but the rocking eighth-note figure in the first violin and viola are enough to recall the similar rocking motion of the first violin at measure 2.
It is in the final measure that the two intervallic polarities combine with greatest effect, bringing the movement to a close with a juxtaposition of ideas more than a resolution of them. Again, we find the C-natural taking special emphasis: it begins the last sonority and continues after the rest of the chord dies out. Therefore we cannot ignore the fact that on some level PC0 is a fundamental reference point throughout the movement—projected contextually, not functionally, through registration and duration.
If we organize the five-note final chord into a set-class, we have 5-7 (0,1,2,6,7). That Webern uses this specific set is significant, since it is the five-note set with the maximum number of possible IC1 and IC5 combined, with three occurrences each:
| Forte Number | Prime Form | IC Vector |
| 5-7 | (0,1,2,6,7) | 3 1 0 1 3 2 |
For the sake of comparison, and to emphasize the significance of this set, only one other five-note set has more occurrences of IC1, the chromatic set 5-1; and only one other five note set has more of IC5, set 5-35. And in each of these cases, the set has none of the counterpart’s IC:
| Forte Number | Prime Form | IC Vector |
| 5-1 | (0,1,2,3,4) | 4 3 2 1 0 0 |
| 5-35 | (0,2,4,7,9) | 0 3 2 1 4 0 |
Thus it would appear that Webern’s choice of set-class 5-7 is either a deliberate attempt to combine the qualities of two opposing intervallic forces, or simply the subconscious result of bringing the musical ideas in the movement to their logical conclusion.
At the start of this analysis I mentioned that IC5 plays an important role in the macro structure of the piece, and named set 4-8 as the one that results from the loudest notes of the piece. It should be noted that this set is related by Kh to set 5-7, the only other group of notes marked with a dynamic equal to or louder than forte. Hence, these sets are tied by both reciprocal complement relation and dynamics, and in one moment an idea that spans the movement is compressed into the final cadence.
Admittedly, a handful of pitches have been left unexplained in the above analysis. Some of these notes can be reasonably arranged to fit into the context of this analysis, and a few of them do not. These will be left for future further investigation. But it should also be noted that none of the other existing analyses avoid this pitfall. The occasional anomaly is to be expected, and rather than try to force every piece of the puzzle into a prefabricated mold, I will set them aside with the hope that the above arguments are convincing with or without these missing pieces.
Finally, I return to Forte’s analysis of the second of Webern’s Bagatelles to address the issue of the last metrically incomplete measure of 5/4. Forte explains:
Alternation of 2+3 and 3+2 forms a regular pattern that is broken at the very end of the movement. Beginning with 2+3, one bar of 2+3 alternates with two bars of 3+2 until the last bar, bar 8, which is in 3/4. Thus, triple meter wins the conflict.10
It does seem that the truncated last measure is making some kind of statement about the meaning of meter in the movement. But, Webern does not indicate a change of meter with a time signature. The idea that there is some “conflict” being resolved at the end makes a strong statement about the character of the movement, one that I don’t think is apparent in the music. If this is a scherzo, or even a commentary on “scherzo” as a musical idea, then perhaps “conflict” is too strong a word. What happens in the final measure does sound more like a “culmination” or a combination of sounds than a resolution of conflict, since the music has too much levity for conflict to take place. When the scherzo idea is combined with the hinted-at V-I “cadence” at measure 2, the wide leaps from one register to the next, the hocketing between first and second violins in the B section, it seems entirely possible to think that Webern wanted the music just to run out.
Bibliography:
Davies, Benjamin K. “The Structuring of Tonal Space in Webern’s Six Bagatelles for String Quartet, Op. 9”. Music Analysis, Volume 26, Issue 1-2, pages 25–58, March-July 2007
Chrisman, Richard. “Anton Webern’s Six Bagatelles for String Quartet, Op. 9: The Unfolding of Intervallic Successions.” Journal of Music Theory Vol. 23, No. 1 (Spring 1979): 81-122.
Forte, Allen. The Atonal Music of Anton Webern. New Haven: Yale University Press, 1998.
Mullin, Carolyn Denise. “Global Coherence in the Selected Atonal Works of Anton Webern.” Ph.D. diss., University of Oregon, 2005.
Perry, Jeffrey. “A Study of Webern’s Six Bagatelles for String Quartet, Op. 9.” Ph.D. diss., Princeton University, 1990.
Pousseur, Henri. “Webern’s Organic Chromaticism.” in Die Reihe, trans. Leo Black. 1958: 51-63.
1Allen Forte, The Atonal Music of Anton Webern (New Haven: Yale University Press, 1998), 169-203.
2Richard Chrisman, “Anton Webern’s Six Bagatelles for String Quartet, Op. 9: The Unfolding of Intervallic Successions,” Journal of Music Theory Vol. 23, No. 1 (Spring 1979): 81-122.
3Jeffrey Perry, “A Study of Webern’s Six Bagatelles for String Quartet, Op. 9,” (Ph.D. diss., Princeton University, 1990).
4Carolyn Denise Mullin, “Global Coherence in the Selected Atonal Works of Anton Webern,” (Ph.D. diss., University of Oregon, 2005), 117-225.
5The descriptions are meant to give only the slightest introduction to the processes by which other analysts have studied Webern’s Bagatelles, as further description is outside of the scope of this paper.
6Forte, 176.
7Chrisman, 118.
8See Henri Pousseur, “Webern’s Organic Chromaticism” in Die Reihe, trans. Leo Black, 1958: 51-63.
9For ease of reading, all musical excerpts in this paper will be reductions in which the first violin appears with stems up in the top staff, second violin stems down, viola stems up in the second staff, cello stems down, and with all rests omitted, unless otherwise indicated.
10Forte, 176.